서포트 벡터 머신(Support Vector Machine, SVM)은 머신러닝에서 가장 강력한 분류 알고리즘 중 하나로, 데이터를 선형 또는 비선형적으로 구분하는 초평면(Hyperplane)을 찾는 방법입니다.
특히, **선형 서포트 벡터 머신(Linear SVM)**은 데이터를 선형적으로 구분할 수 있는 경우에 가장 적합하며, 마진(Margin)을 최대화하는 방식으로 최적의 결정 경계를 찾습니다.
SVM에서 마진을 최적화하는 방법에는 두 가지가 존재합니다:
- 하드 마진(Hard Margin) 분류
- 소프트 마진(Soft Margin) 분류
이 글에서는 두 가지 마진 분류 방법의 개념과 차이점, 적용 방법을 설명합니다.
📌 목차
- 서포트 벡터 머신(SVM) 개요
- 마진(Margin)이란?
- 하드 마진(Hard Margin) 분류
- 개념 및 특징
- 적용 방법
- 한계점
- 소프트 마진(Soft Margin) 분류
- 개념 및 특징
- 적용 방법
- 장점
- 하드 마진 vs. 소프트 마진 비교
- 결론
1. 서포트 벡터 머신(SVM) 개요
SVM은 데이터를 가장 잘 구분할 수 있는 초평면(Hyperplane)을 찾는 알고리즘입니다.
✅ 초평면(Hyperplane)
- 데이터를 구분하는 결정 경계(Decision Boundary).
- 선형 SVM에서는 **직선(2D), 평면(3D), 초평면(nD)**으로 표현됨.
✅ 서포트 벡터(Support Vectors)
- 결정 경계를 형성하는 가장 중요한 데이터 포인트들.
- 이 서포트 벡터를 기준으로 마진을 최대화함.
💡 SVM의 목표:
➡️ 마진(Margin)을 최대화하는 초평면을 찾는 것!
➡️ 마진이 클수록 새로운 데이터에 대한 일반화 성능이 좋아짐.
2. 마진(Margin)이란?
마진은 초평면과 가장 가까운 데이터 포인트(서포트 벡터) 간의 거리를 의미합니다.
✅ 마진이 넓을수록 일반화 성능이 좋음
✅ 마진이 좁을수록 과적합(Overfitting) 가능성이 높음
마진을 최적화하는 방법에는 하드 마진(Hard Margin)과 소프트 마진(Soft Margin) 두 가지가 있음.
3. 하드 마진(Hard Margin) 분류
🔹 개념 및 특징
하드 마진 분류는 완벽한 선형 분리가 가능한 경우에 적용되는 방법입니다.
✅ 특징
- 데이터가 100% 분리 가능해야 함.
- 마진을 최대화하여 초평면을 설정.
- 초평면 근처에 오차(Noise)가 허용되지 않음.
🔹 적용 방법
하드 마진은 모든 데이터 포인트가 결정 경계 밖에 위치하도록 하는 제약 조건을 설정하여 학습됩니다.
수학적 정의
초평면의 방정식을 다음과 같이 정의합니다:
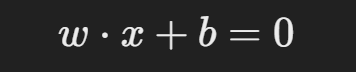
마진을 최대화하는 것이 목적이며, 제약 조건은 다음과 같습니다:
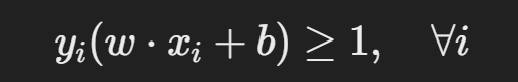
여기서,
- xi = 데이터 포인트
- yi = 클래스 라벨 (+1 또는 −1)
- w = 가중치 벡터
- b = 절편
이 제약을 만족하는 가장 큰 마진을 찾기 위해, 다음 최적화 문제를 풀어야 함:
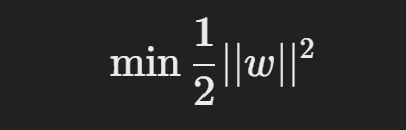
🔹 하드 마진의 한계점
❌ 실제 데이터는 대부분 완벽하게 선형 분리가 불가능
❌ 이상치(Outlier)가 존재하면 모델이 심각하게 영향을 받음
❌ 오버피팅(Overfitting) 발생 가능
➡️ 따라서, 대부분의 실제 문제에서는 소프트 마진(Soft Margin)을 사용함!
4. 소프트 마진(Soft Margin) 분류
🔹 개념 및 특징
소프트 마진 분류는 완벽한 선형 분리가 불가능한 경우에도 적용 가능합니다.
✅ 특징
- 일부 데이터 포인트가 마진을 벗어나도록 허용.
- 오차(슬랙 변수, Slack Variable) 허용으로 인해 유연한 분류 가능.
- 이상치(Outlier)의 영향을 줄일 수 있음.
🔹 적용 방법
소프트 마진에서는 제약을 완화하여 일부 데이터가 초평면을 넘을 수 있도록 함.
수학적 정의
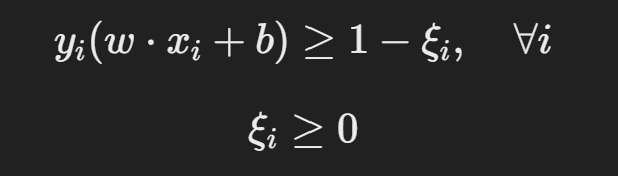
여기서,
- ξi (슬랙 변수): 초평면을 넘은 데이터의 오차를 허용하는 변수.
- C (Regularization Parameter): 오차 허용 정도를 조절하는 하이퍼파라미터.
최적화 문제는 다음과 같이 변경됨:
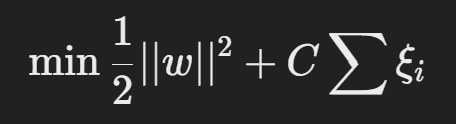
➡️ C 값이 크면: 마진을 좁히고 오류를 줄이는 방향으로 학습 (Overfitting 위험 증가)
➡️ C 값이 작으면: 마진을 넓게 유지하여 일반화 성능 향상 (Underfitting 위험 증가)
🔹 소프트 마진의 장점
✅ 완벽한 선형 분리가 필요하지 않음
✅ 이상치(Outlier)에도 강함
✅ 실제 데이터에 적용하기 적합
5. 하드 마진 vs. 소프트 마진 비교
| 비교 항목 | 하드 마진(Hard Margin) | 소프트 마진(Soft Margin) |
|---|---|---|
| 선형 분리 가능 여부 | 선형 분리가 100% 가능해야 함 | 일부 오차 허용 |
| 오차(Noise) 허용 여부 | 불가능 (오차 허용 없음) | 가능 (오차 허용) |
| 이상치(Outlier) 영향 | 민감함 (오버피팅 위험) | 비교적 안정적 |
| 적용 사례 | 데이터가 완벽히 분리 가능할 때 | 현실적인 데이터에서 유용 |
6. 결론
✅ 하드 마진(Hard Margin): 완벽한 선형 분리가 가능한 경우 사용, 하지만 현실에서는 적용이 어려움.
✅ 소프트 마진(Soft Margin): 오차를 허용하여 보다 유연한 분류를 수행, 실전에서 가장 많이 사용됨.
💡 요약
- 현실적인 데이터는 대부분 완벽한 선형 분리가 어렵기 때문에 소프트 마진이 더 적합.
- C 파라미터를 조정하여 일반화 성능을 최적화할 수 있음.
🚀 SVM을 활용한 머신러닝 분류 모델을 만들 때, 데이터 특성에 맞는 마진 전략을 선택하는 것이 중요합니다! 😊
